Eigenvalue Problems
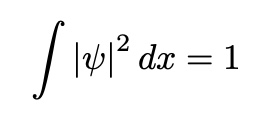
-Schodinger Equation
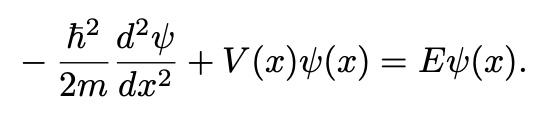Time-Independent Shrodinger Equation
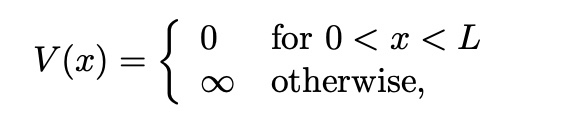
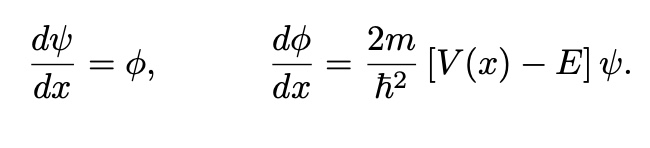
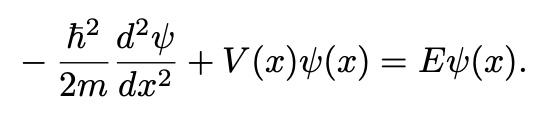Time-Independent Shrodinger Equationwith Infinite Square potential
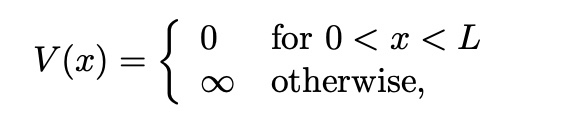
then Boundary condition
to Solve TISE
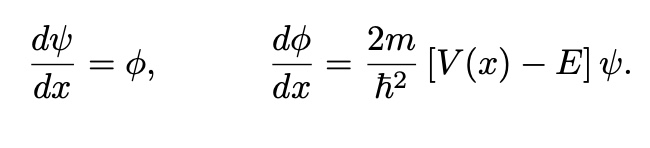
in order to solve problem,
Change the Energy E
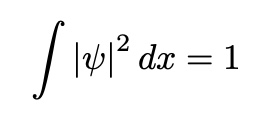
# Schrodiger Equation
import numpy as np
import matplotlib.pyplot as plt
# Potential ftn
def V(x):
# Infinite Potential Well
return 0.0
def f(r, x, E):
psi=r[0]
phi=r[1]
fpsi=phi
fphi=(2*m/h_bar**2)*(V(x)-E)*psi
return np.array([fpsi, fphi], float)
def RK4(r, x, E):
global h
k1=h*f(r, x, E)
k2=h*f(r+0.5*k1, x+0.5*h, E)
k3=h*f(r+0.5*k2, x+0.5*h, E)
k4=h*f(r+k3, x+h, E)
r+=(k1+2*k2+2*k3+k4)/6
return r
def solve(E): # find psi=0
global L
psi=0.; phi=1.
r=np.array([psi, phi], float)
for x in np.arange(0, L, h):
r=RK4(r, x, E)
return r[0]
if __name__=="__main__":
m=9.1094e-31
h_bar=1.0546e-34
e=1.6022e-19
L=5.2918e-11 # Bohr radius
N=1000
x=np.linspace(0, L, N)
h=x[1]-x[0]
E1=0*e; E2=1*e
psi2=solve(E1)
tolerance=e/1000
while abs(E2-E1)>tolerance:
psi1, psi2=psi2, solve(E2)
E1, E2=E2, E2-psi2*(E2-E1)/(psi2-psi1)
print("E=", E2/e, "eV")
pphi=np.zeros_like(x)
ppsi=np.zeros_like(x)
pphi[0]=1.; ppsi[0]=0.
for i in range(len(x)-1):
r=np.array([ppsi[i], pphi[i]], float)
r=RK4(r, x[i], E2)
ppsi[i+1]=r[0]
pphi[i+1]=r[1]
# Normalize psi
integ=0.
for i in range(len(x)):
integ+=h*ppsi[i]**2
norm_ppsi=ppsi/np.sqrt(integ)
plt.plot(x, norm_ppsi)
plt.xlim(0, L)
plt.show()